


In Artificial Intelligence a hill-climbing algorithm is an algorithm used to optimize mathematical problems. It keeps increasing its value continuously until a peak solution is achieved.
Hill climbing algorithm can be defined as a local search algorithm which is a form of the heuristic search algorithm. It keeps moving upward from the current state or the initial state until the best solution is attained or the peak is reached. Let us have a general example for a better understanding
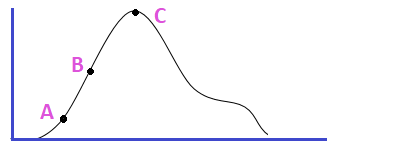
Suppose Mr.X is climbing a hill. Mr.X will keep climbing the hill until he reaches the top of the hill. Mr. X is now at point A so the current position of Mr. X is A. Later he is at point B which is a better position than point A. So the current position of Mr. X now points to B. This procedure is continued until he reaches point C which is the peak of the hill. S in terms of our algorithm the current state is A initially and gets a better state B than A then the algorithm changes the current state from A to B this will be continued until it attains the best solution or the best point. Initially, the starting point is referred to as the base of the hill which is a non-optimal state. And it tries to climb or iterate constantly until it reaches the peak value or a certain precondition. The process of improving the current state can be called climbing. This is why it is named a hill-climbing algorithm.
Hill climbing algorithm can be said as a memory-efficient way to solve large computational problems. The best example for a hill-climbing approach is the Travelling Salesman Problem. The Hill climbing approach may not be the way to find the optimal solution but it is good to calculate the local minima/maxima.
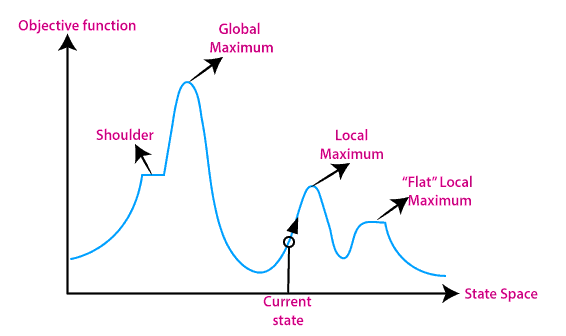
The above given is a graphical representation of states and the objective function. If the y-axis represents the objective function then we can establish the global/local maxima. If the y-axis is used to represent the cost function we can establish the local/global minima. The x-axis is used to represent the state-space.
The following are the key features of the hill-climbing algorithm
It is the simplest implementation of a Genetic Algorithm. While comparing with more traditional genetic algorithms, It has a faster iteration but is less thorough than those.
Working on hill climbing is very simple. Let us have a simple description of the work.
The following are the types of hill-climbing algorithms:

It is the simplest form of the hill-climbing method where the neighboring solutions are evaluated. If the neighbor state holds a value greater than the current state then the algorithm will set this neighbor state as the current state. It checks only one successor state at a time. Following are the features of this algorithm:
Step 1:Create a CURRENT node, NEIGHBOR node, and a GOAL node.
Step 2:Evaluate the CURRENT node, If it is the GOAL node then stop and return success.
Step 3:Else set the NEIGHBOR node as the CURRENT node and move ahead.
Step 4:Loop until CURRENT node = GOAL node or there exist no operator to apply.
Step 5:EXIT.
It is a variation of the simple hill-climbing algorithm. Here the algorithm will check all the neighboring nodes of the current state and select the one with the value closest to the goal state. As it searches all the neighboring nodes the time consumption is high and also the consumption power is also high.
Step 1:Create a CURRENT node, NEIGHBOR node, and a GOAL node.
Step 2:Evaluate the CURRENT node, If it is the GOAL node then stop and return success.
Step 3:Else set a state (X) where the current state successors have higher values than it.
Step 4:Operate with the new operator and generate a new solution.
Step 5: Compare this new solution with the GOAL node. If yes then EXIT the program, Else compare it with the state (X).
Step 6:If the new state is higher than the state (X), then set it as X
Step 7:Continue the loop. Repeat steps 4 and 5.
Step 8:EXIT.
Here the algorithm never focuses on all the neighboring nodes. It selects one neighboring node randomly to check whether it is better than the current node. The selection of neighboring nodes randomly is performed based on some pre-defined criteria.
Step 1:Create a CURRENT node, NEIGHBOR node, and a GOAL node.
Step 2:Evaluate the CURRENT node, If it is the GOAL node then stop and return success.
Step 3:Else select a NEIGHBOR node randomly and evaluate NEIGHBOR.
NEIGHBOR is selected with probability 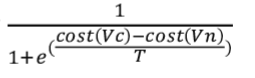
Step 4: If NEIGHBOR = GOAL return success and exit. Else set CURRENT node=NEIGHBOR and continue the loop. Repeat steps 2, 3, 4
Step 5:EXIT.
Here a try-and-try strategy is used. Here the nodes are searched iteratively and then selects the best one at each step. This will continue until the goal is found. The success of the procedure depends on the shape of the hill. With a few plateaus, local maxima, and ridges it is easy to get to the destination. It is also known as shotgun hill climbing. A successful algorithm with probability p runs n times or a solution is found, will solve with probability 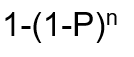
There are three main regions in which the hill-climbing algorithm cannot attain an optimal solution.
At the point of local maximum, the greedy approaching feature of the algorithm will lead to a termination since the neighboring states have a value lower than the current state. But this is not the best possible solution, there exists a global maximum.
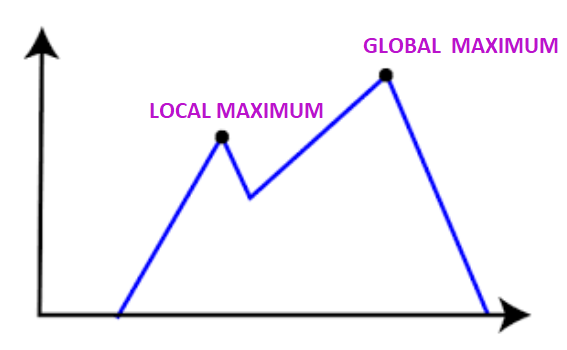
Solution: The backtracking technique can be used to overcome the problem of the local maximum. The visited states are listed and if the search reaches an undesired state, it can backtrack and explore a new path.
Points on ridge always look like a peak. All the possible moves from a point on the ridge are downward. So, the algorithm will terminate from such a state.
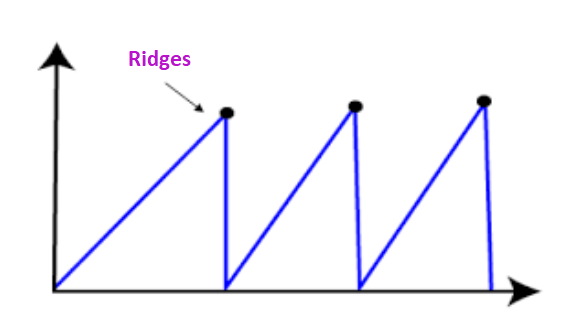
Solution: Make movements in several directions at once.
On the plateau, all the neighbors are with the same value. So it is difficult to select the best direction.
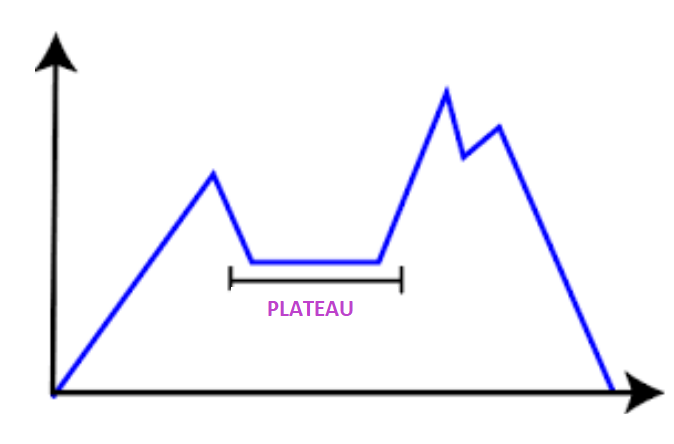
Solution: Take a huge jump to reach a non-plateau space.
As we know the hill-climbing algorithm never makes a downward movement or a move towards a lower value. And is incomplete since it will be stuck on a local maximum. If the algorithm makes a random walk, then it can be complete but not efficient.
Simulated annealing is a solution or an algorithm that allows downward steps for escape from local maxima.
Annealing can be defined as the process of hardening a metal to a high temperature then cooling gradually, So the metal will reach a low-energy crystalline state mechanically. A similar process is used in the simulated annealing. Here the algorithm picks a random move rather than the best move. If the selected random move improves the state, then the same path is followed. Else it follows a path with a probability of less than 1, or it will make a move downward and choose another path.
The following areas can make use of the hill-climbing algorithm.
MARKETING
It can be used to generate good marketing plans. This technique is widely used to solve Travelling Salesman Problems. It can be used to establish the local minima efficiently.
ROBOTICS
It can be used to enhance the coordination of different components and systems in robots.
JOB SCHEDULING
In job scheduling, the system resources are allocated to different tasks and there is a migration of jobs from one node to another. Hill climbing can be used to establish the right route.