
In this tutorial on recursion, you will master everything about a unique process in a function called Recursion. Also, you will see some problems that are well suited to be solved by recursion, such as number factorial, Fibonacci series, etc.
Recursion, generally, means the process of the repetitive calling of a function by itself to work on smaller problems. A function is said to be recursive if a function calls itself and such function calls are named as recursive calls. Precisely, the recursive calls end when it reaches the base case.
In C, Recursion and iteration go hand in hand but both notch some specific tasks designed for them. For instance, recursion is useful for performing some mathematical calculations, sorting, searching, traversing, etc. However, it is not applicable to all problems. So we can say that it is nothing but a type of customized function. Some problem that well
The use of recursion in C is an elegant way to reduce the code size. But the fact is that it is difficult to understand the working. Here is its prototype:
void recurse() // recursive function
{
........
recurse(); //recursive call
........
}
main() {
........
recurse(); // function call
........
}
Working of recursion can be best visualized as below to make it more understandable.
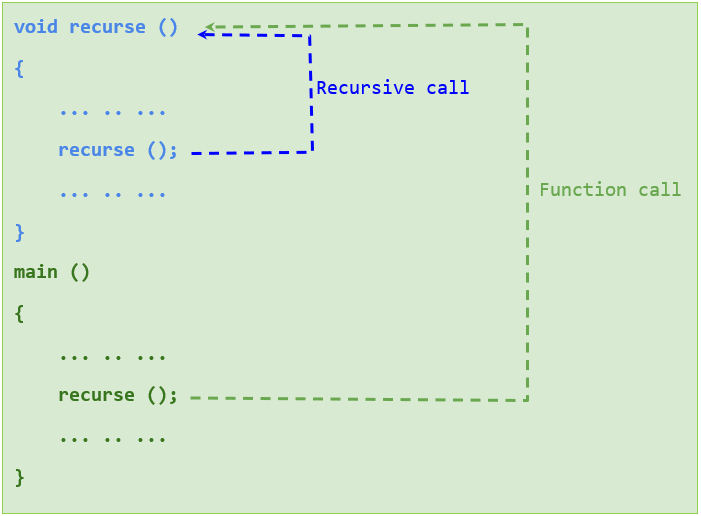
We have already learned that in C execution begins with the main function, as it traverses when it comes across a function call, the control will shift to the corresponding function. We can see that the calling of a function is performed in a cycle just like a loop. As we know that there must be an exit status in every loop; otherwise it will turn into an infinite one. A recursive function is not an exception either.
In the architecture of recursive function, it has got two inevitable components. They are :
Find below a simple program that will sum all the numbers up to the defined one, through a recursive function.
#include
int sum(int n);
int main()
{
int num, tot;
printf(" Calculate sum of the numbers upto:-> ");
scanf("%d", &num);
tot= sum(num);
printf("\n The result is %d", tot);
}
int sum(int n)
{
if (n !=0)
return (n + sum(n-1));
else
return n;
}
Output:
Calculate sum of the numbers upto:-> 5 The result is 15
Calculate sum of the numbers upto:-> 10 The result is 55
This recursion continues till the variable 'no' reaches '0'. As it happens, the compiler will exit the program. Suppose we enter 5. The main function will pass the number as an argument. Then the number is decreased to 4 and again the function is called. Thus, the addition of 5+4+3+2+1 takes place resulting in 15.
Lets breakdown the above program of the recursive method call by the figure shown below:

We can determine the factorial of any number with the help of recursion. Mathematically factorial of a number n is defined as
n! = n x (n-1) x (n-2)......x 2 x 1
| Generalised way of finding factorial | Example: 5! |
|---|---|
| n!= n x (n-1)! | 5! = 5 x 4! |
| n!= n x (n-1) x (n-2)! | 5! = 5 x 4 x 3! |
| n!= n x (n-1) x (n-2) x (n-3)! | 5! = 5 x 4 x 3 x2! |
| 5! = 5 x 4 x 3 x2 x1! | |
| n!= n x (n-1) x (n-2) x (n-3) ….3! | 5! = 5 x 4 x 3 x2 x1 =>120 |
| n!= n x (n-1) x (n-2) x (n-3) ….3 x 2! | |
| n!= n x (n-1) x (n-2) x (n-3) ….3 x 2 x1! |
We can observe that the problem is divided into subproblems which use the same function and repeats until it reaches the base value.So on each call integer is multiplied by the next smaller one repeatedly until it reaches the lowest value '1'. Now we can construct a recursive function 'fact' like this:
#include
int fact( int n)
{
if(n <= 1)
return 1;
else
return n * fact(n - 1);
}
main()
{
int i;
printf (" Calculate factorial of --> ");
scanf("%d",&i);
printf("Factorial of %d is %d\n", i, fact(i));
}
Output:1 Calculate factorial of --> 5 Factorial of 5 is 120 Output:2 Calculate factorial of --> 10 Factorial of 10 is 3628800
Suppose we enter 5 as input.
The following figure will give you a clear picture of recursion to employ factorial of a number in c.

Fibonacci series is a series of positive integers, where each term is the sum of the previous two terms. The series has intense mathematical significance. Fibonacci series starts with numbers 0 and 1 and the sequence is as demonstrated below:
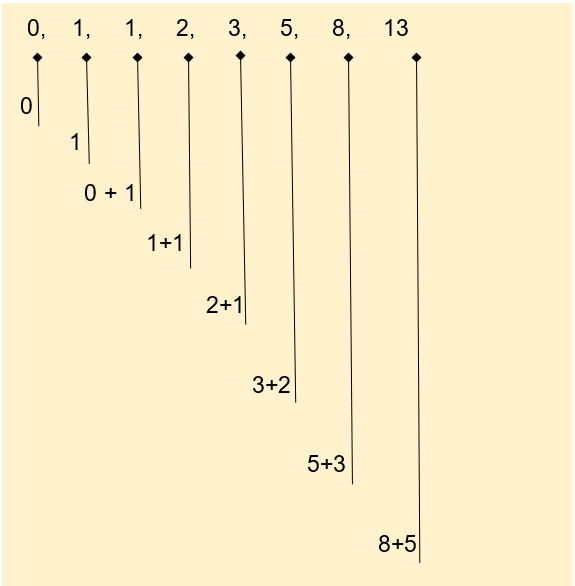
Here is a sample program using iteration to execute the fibonacci series:
#include
int main()
{
int i, n, c = 0, p = 1, t = 0;
printf( " How many terms do you want to show -> ");
scanf("%d", &n);
printf("Fibonacci Series: ");
for (i = 1; i <= n; ++i)
{
printf("%d, ", t);
t = c + p;
p = c;
c = t;
}
return 0;
}
In this program c can be considered as current value and p can be taken as previous value. we have initialized c as 1 and p as 0. Also the total is stored in variable t which is initialized to 0.Here for loop is used to prevent the iteration from infinite execution. In the first cycle of for loop:
it prints the value of t = 0, then
t=0 +1=1
p= 0
c= 1
In the next section cycle:
print "1" (value of t)
t= 1+1=2
p= 1
c= 2
.. and so on.
Now using recursion we can do the same with fewer codes. What we have to do is define a function "fibn" and call it inside itself with proper arguments.
int fibn (int i)
{
if(i == 0)
return 0;
if(i == 1)
return 1;
else
return fibn(i-1) + fibn(i-2);
}
main()
{
int i, n,a;
printf( " How many terms do you want to show -> ");
scanf("%d", &a);
printf("Fibonacci Series: ");
for (i = 0; i < a; i++)
printf("%d, ", fibn(i));
}
This program will produce exactly the same result as before. fibn(i) will be called 'a' number of times as specified by the end user and will recursively call the function to produce the exact result till it reaches the end.
