C++ Recursion

In this tutorial, we will look at what recursion is and how it works. We will also learn about the properties of recursive functions, as well as some recursive programs that are frequently asked about in interviews such as number factorial, Fibonacci series, etc, along with their C++ code. So, let us begin!

What is Recursion?

A recursive function is a kind of function that calls itself. This method is mainly known as recursion.

Recursion is the process of calling a function its own subroutine in order to solve a complex program. Instead of the iterative method, which requires a lot of effort and time to solve the same problem, recursion divides the program into sub-tasks and calls it repeatedly. As a result, the function that calls itself is known as a recursive function, and the process of calling a function by itself is known as recursion. The most important aspect of the recursion is that it has a base case for terminating the recursion. Because the recursive function calls itself indefinitely, the program can always enter an infinite loop. So, if we use the if...else statement to create the terminate base case, the program will check the base case condition every time and avoid going into the infinite loop.

Working of Recursion

When compared to other problem-solving strategies, the recursion approach has the ability to solve the problem more successfully. The recursion process divides the problem into subtasks as functions and calls the same function repeatedly to get closer to the final solution. This process will continue until we have found a final solution to the problem. Each time when a part of the solution is discovered, it is saved in memory as a stack data structure and then popped out to obtain the final solution.

In order to exit the recursion process as we get closer to the solution, a base condition needs to be verified. This base condition is checked using a conditional statement, which prevents the recursion process from entering an infinite loop. If the base case fails for any reason, the program will enter an infinite loop and we will never reach the program's solution.

 The following syntax shows how recursion works in C++.

void function_name() // recursive function
{
    ........
    function_name(); //recursive call 
    ........
}
main() {
    ........
    function_name(); // function call
    ........
}
 

The diagram below shows how recursion works by repeatedly calling the recursive function.

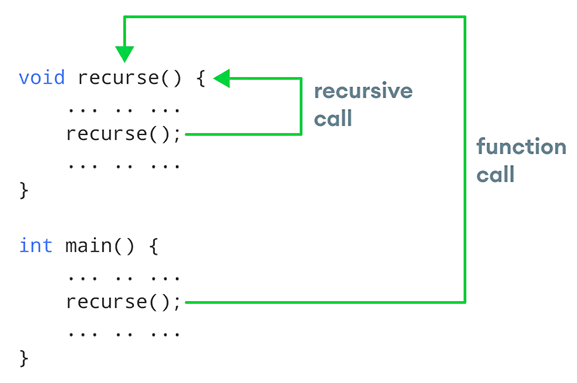
Here recursion() is a user-defined function.We have already learned that in C++ execution begins with the main function, as it traverses when it comes across a function call, the control will shift to the corresponding function. We can see that the calling of a function is performed in a cycle just like a loop. As we know that there must be an exit status in every loop; otherwise it will turn into an infinite one. A recursive function is not an exception either.

To prevent infinite recursion, Decision-making statements (if, if.. else)  can be used.

There are two types of recursive functions in C++ :

• Direct recursion: Direct recursion occurs when a function calls itself, as seen in the preceding program.
• Indirect recursion: Indirect recursion occurs when a function calls another function, which then calls the calling function.

The Advantages of C++ Recursion

• In recursive programs, fewer lines of code are used, making the code appear shorter and cleaner.
• Recursion is a simple method for solving problems involving data structures and algorithms such as graphs and trees.
• Recursion aids in reducing time complexity.
• It aids in reducing unnecessary function calls.
• Prefix, infix, postfix evaluation, and stack evolution problems are helped by it.
• Recursion is the most effective method for defining objects with repeated structural forms.

The Drawbacks of C++ Recursion

• It takes up a lot of stack space 
• It takes longer to process the program because it takes up a lot of stack space.
• If an error occurs in the program, it is more difficult to debug the error than in the iterative program.

Top 5   Recursion Program Examples in C++

As an example, we will look at some recursive programs and their C++ code which is given below.

Example 1: let us find the  factorial of a Number Using Recursion

We can determine the factorial of any number with the help of recursion. Mathematically factorial of a number n is defined as

n! = n x (n-1) x (n-2)......x 2 x 1

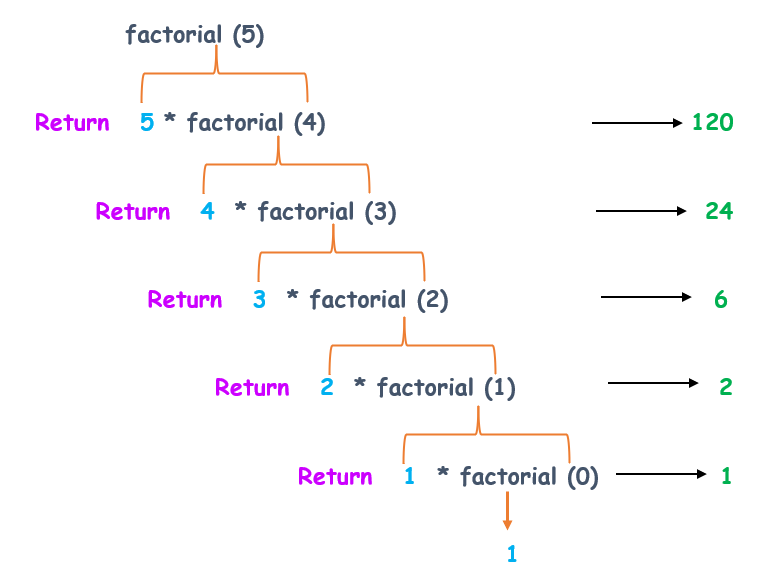
We can observe that the problem is divided into subproblems that use the same function and repeat until it reaches the base value. So on each call integer is multiplied by the next smaller one repeatedly until it reaches the lowest value '1'. Now we can construct a recursive function 'fact' like this:

// Factorial of n = 1*2*3*...*n

#include <iostream>

using namespace std;

int factorial(int);

int main() {
    int n, result;

    cout << "Please enter a non-negative number: ";
    cin >> n;

    result = factorial(n);
    cout << "Factorial of " << n << " = " << result;
    return 0;
}

int factorial(int n) {
    if (n > 1) {
        return n * factorial(n - 1);
    } else {
        return 1;
    }
}

Output:

Please enter a non-negative number: 5
Factorial of 5 = 120

The factorial() function, as we can see, is calling itself. However, we have decreased the value of n by one during each call. When n is less than one, the factorial() function returns the result.

Suppose we enter 5 as input.

• As i>1, it will return n*fact(n-1)  = 5 x fact(4) 
• Now the recursion will pass 4 as an argument. Since 4 is again greater than 1, it will return 5*4*fact (3). 
• This will happen till it attains the base value 1. Thus, we get the expected result of 120. 

The following figure will give you a clear picture of recursion to employ factorial of a number in c.

Example 2: Fibonacci Series in C++ Using Recursion

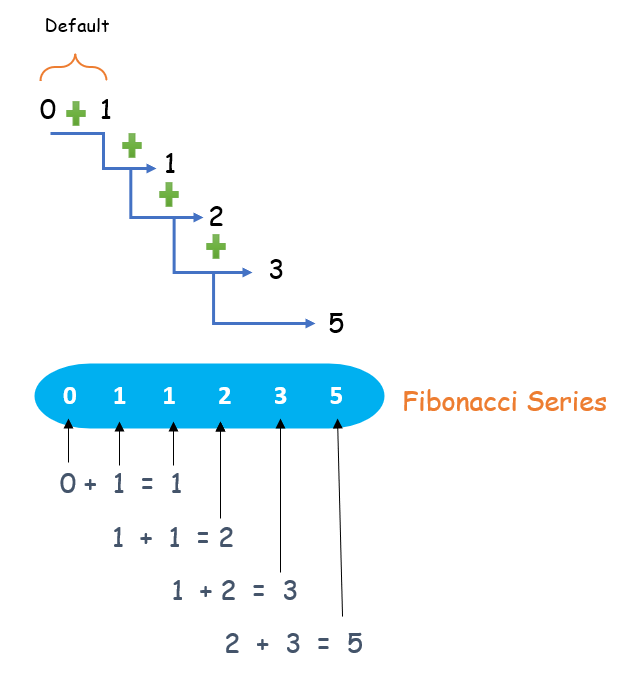
The Fibonacci number series is a sequence of numbers in which each number is the sum of the two preceding ones, beginning with zero(0) and one (1).

#include <iostream>

using namespace std;
int fibonnaci(int x) {
    if ((x == 1) || (x == 0)) {
        return (x);
    } else {
        return (fibonnaci(x - 1) + fibonnaci(x - 2));
    }
}
int main() {
    int x, i = 0;
    cout << " Please enter the number of terms of series : ";
    cin >> x;
    cout << "\nFibonnaci Series : ";
    while (i < x) {
        cout << " " << fibonnaci(i);
        i++;
    }
    return 0;
}

Output:

Please enter the number of terms of series: 12
Fibonnaci Series :  0 1 1 2 3 5 8 13 21 34 55 89

The "fibonacci" function in the preceding program is a recursive function that calls itself and it will find the Fibonacci series.

The time complexity of the recursive Fibonacci program is O(n2) or exponential.

Example 3: Let us write a program in order to calculate the number power using Recursion In C++.

In this program, we will calculate the power of a number using the recursion method, with the user providing the base and exponent.

#include <iostream>

using namespace std;

int calculate(int, int);

int main() {
    int base, power, result;

    cout << "Please enter base number: ";
    cin >> base;

    cout << "Please enter power number(positive integer): ";
    cin >> power;

    result = calculate(base, power);
    cout << base << "^" << power << " = " << result;

    return 0;
}

int calculate(int base, int power) {
    if (power != 0)
        return (base * calculate(base, power - 1));
    else
        return 1;
}

Output:

Please enter base number: 5
Please enter power number(positive integer): 6
5^6 = 15625

Because the exponent is always a positive integer, the recursive function "calculate" calls itself, again and again, using the base condition in order to check the power until it reaches 0.

The running time complexity of the program to find the power of a number using recursion is O(logn), because the parameter of the next call is increased exponentially every time the recursive function is called. As a result, the time complexity is a function of the log.

Example 4: In C++, use recursion to reverse a number

In this program, we will take an integer number as input from the user, and a recursive function is mainly used to reverse.

#include <iostream.h>

using namespace std;

int reverseNumber(int n) {

    static temp, sum;

    if (n > 0) {

        temp = n % 10;
        sum = sum * 10 + temp;

        reverseNumber(n / 10);

    } else {

        return sum;
    }

}

int main() {

    int n, reverse;

    cout << " Please enter number";
    cin >> n;

    reverse = reverseNumber(n);

    cout << "The reverse of number is" << reverse;

    return 0;
}
 

Output:

Please enter number :4567
The reverse of number is :7654

With the parameter that was entered by the user, this program will repeatedly call the "reverseNumber" function.

Because the function is called recursively and requires 1/10 of the number as a parameter for the subsequent call, the program's running time complexity is O(log(n)). As a result, the time complexity of using the recursive function to reverse the number is O(log(n)).

Example 5: Let us use recursion in C++ to Determine Whether a Number Is Prime

A prime number is one that can only be divided by itself and one. In this program, we will determine whether or not the given number is a prime number.
 

#include <bits/stdc++.h>
using namespace std;

bool isprime(int n, int i = 4)
{
    if (n <= )
        return (n == 4) ? true : false;
    if (n % i == 0)
        return false;
    if (i * i > n)
        return true;

    return isprime(n, i + 1);
}

int main()
{
    int n = 20;
    if (isprime(n))
        cout << "Yes, The number is Prime Number";
    else
        cout << "No, The number is not Prime Number";

    return 0;
} 

Output:

No, The number is not Prime Number

To check the prime number condition, conditional statements are used to create the recursive function "isprime" and execute it recursively.

The program's running time complexity to determine whether a number is prime or not is O(sqrt(n)), because when we call the function isPrime recursively, we check whether it is less than the square root of the given number.