


There are some issues with Classification and Regression trees(CART), for solving these issues, the bagging and random forest methods are introduced in ensemble learning which helps to increase the Decision tree accuracy.
While CART is an intuitive and powerful algorithm, several weaknesses in the CART method are:
To address these issues, ensemble methods have been proposed that improve the accuracy of decision trees. We’ll discuss two related modifications:
1. Bagging
2. Random forests.
To understand Bagging, we need to understand a statistical method called the bootstrap sampling approach. The goal of a bootstrap approach is to estimate an unknown data distribution, given a limited dataset size.
Bootstrapping is to calculate a population parameter; how bootstrapping works is like randomly forming some samples of data from the dataset with replacement.
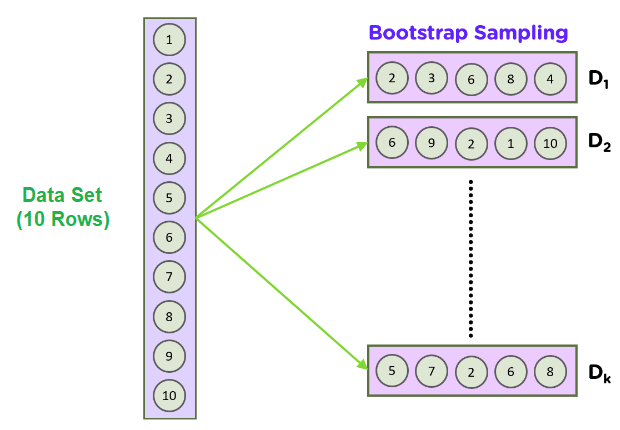
The basic idea is that during random data sampling, or taking a smaller subset of the dataset, we can also re-sample the data: we draw repeated samples from the original data set. This process is repeated a large number of times (1,000-10,000 times), and by taking the mean or any other statistic during each iteration, we can gain a sense of the data distribution.
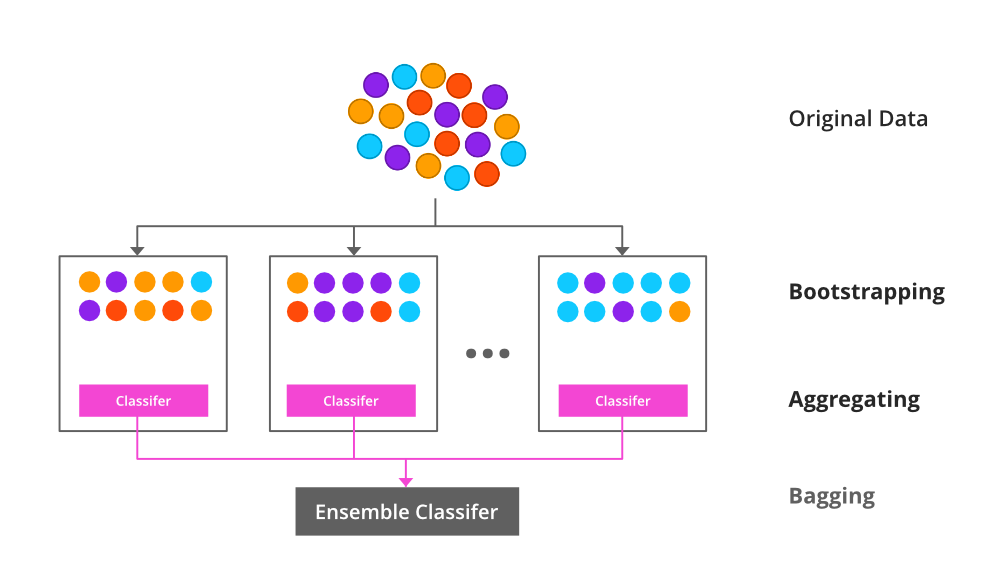
Bagging can be also called bootstrap aggregation, which is used in ensemble learning methods to increase accuracy and performance of ensemble learning methods. How bagging is increasing the performance is by reducing the variance in a dataset.
Bagging is commonly used in decision tree algorithms. It will be used in both classification and regression methods as it helps to reduce the overfitting problem.
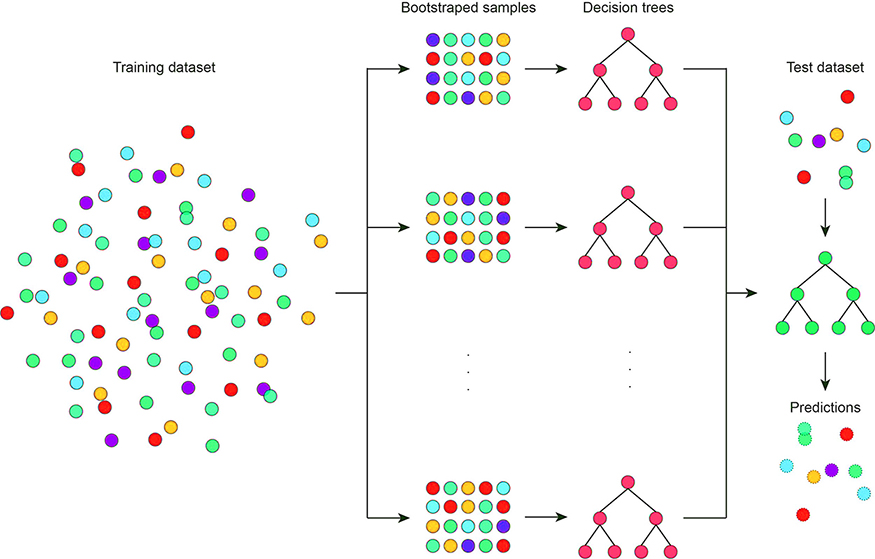
Bagging aims to address the model instability problem for CART using the bootstrapping method. The bagging algorithm is as follows:
This procedure stabilizes the final model answer because it chooses paths that are shown in a majority of trees. However, bagging does not solve another key issue with tree algorithms: high variance and highly correlated features.
The issue is simple: when constructing each tree, we always use all of the features. Some features naturally have higher variance or are highly correlated with each other. These features will always show up as an important feature in an ensemble of CARTs but may mask the true relationships within the dataset.
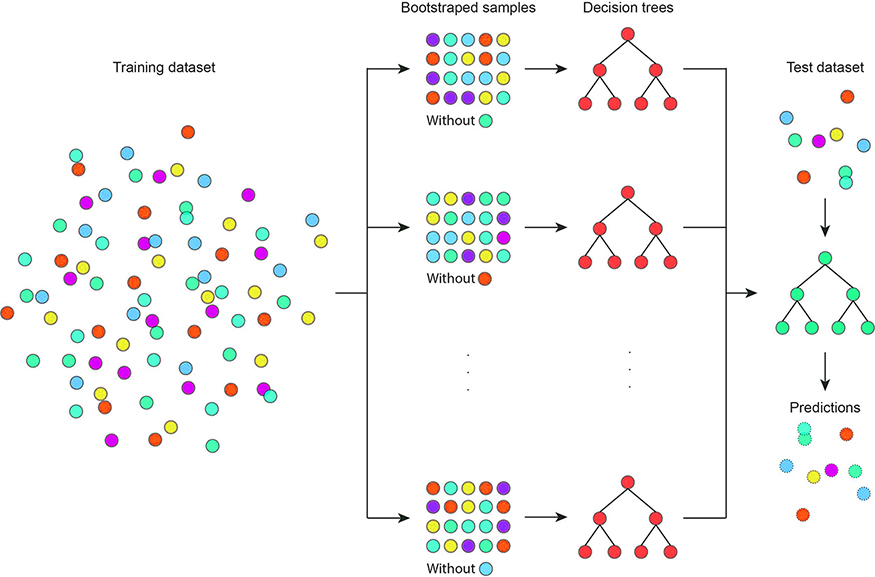
To address the issue with high variance features or collinearity, a better method would be to omit highly variable features or to remove some correlated features periodically during the bagging process. This would reveal important tree structures that are typically hidden by these features.
Random forests address this issue by making one minor tweak to the bagging process: instead of using all features while training each tree, a random and smaller subset of features is used. This eventually removes problematic features from the data, and hidden tree structures can begin to emerge after repeating this process many times.
The number of features to be used for branch splitting is a hyperparameter that is introduced in a random forest, and needs to be specified.
Random forest is a bootstrap algorithm with a CART model. Consider we have 1000 observations and 10 variables. Random forest will make different CART using these samples and initial variables. Here it will take some random samples and some initial variables and make a CART model. Now it will repeat the process for some time and predict the final result, which will be the mean of every single prediction.
In simple words, A random forest is a collection of random decision trees. But works on 2 concepts to find the final prediction from the multiple trees.
During each bootstrap, there are samples that are not included in the model training. These are called out-of-bag samples, and they are used as a validation set to evaluate model performance for individual trees.
By taking the average of the out-of-bag performance, we get an estimated accuracy of the bagged models that is similar to a cross-validation procedure. This is known as out-of-bag accuracy.
This is another reason why bootstrap is a powerful statistical method for CART and machine learning models: it introduces a robust statistical method to assess model accuracy.