


Support vector machines are one of the most popular and used supervised machine learning algorithms which is mainly used for classification, but it can be used for both classification and regression type problems. It gets popular because of its good accuracy and less computational cost.
As we know, the classification is categorizing the data into different categories and we need to have a clear and precise line to make the data into categories, support vector machines are doing it by making a clear line of boundary, which we call a hyperplane. With the help of that boundary line, we can categorize the new data easily into different categories.
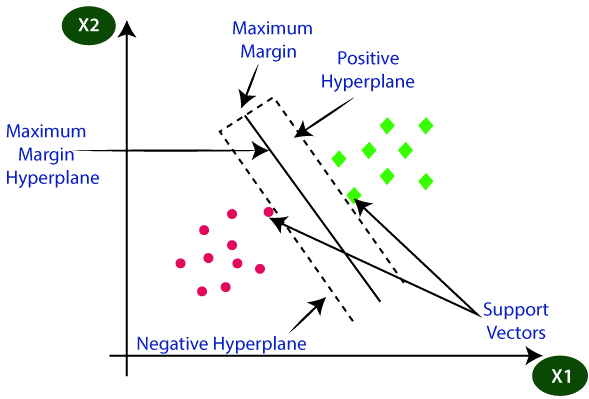
Hyperplanes are created with the help of support vectors. Support vectors are the points that are extreme which we have chosen to make the hyperplane. We are using these support vectors for deciding the hyperplanes hence we call this machine-learning algorithm a support vector machine.
From the below picture you can understand the hyperplane and the categories that are divided based on the hyperplane.
Now let us make it more clear by checking a simple example. Let us consider we have some tigers and lions and we have a strange tiger that has some resemblances with the lions. In this case, we need a model that can clearly categories the tigers and the lions. For that, we need the help of Support vector machines which will be trained with a lot of images of tigers and lions so that it can categorize the lions and tigers properly.
Now we show the stranger tiger to the SVM and it makes the hyperplane by taking the extreme points in both tigers and lions and then create a decision between the tigers and lions and finally on the basis of support vectors and hyperplanes it classifies the strange tiger as a tiger.
Mostly the application of the support vector machine comes in the area of face detection, image categorizing, etc.
First, let’s take the example of a binary classification problem shown below that aims to identify a decision boundary between the solid and empty data points:
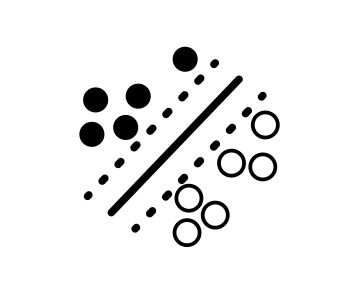
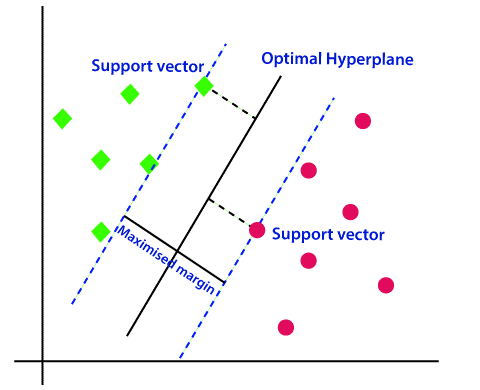
The support vectors are the data points that lie closest to the decision boundary (solid line). They are the most challenging data points to classify and directly determine the position of the decision boundary.
Goal: Maximize the margin between two classes
A support vector machine aims to maximize the margin (dotted line) between the support vectors of the different classes. In other words, we’re trying to see how to identify a decision boundary that can separate the data best.
How does it maximize the margin? It does this through constrained optimization methods - methods that optimize some objective function with respect to constraints that represent limitations that we define.
The mathematics to understand the optimization steps requires extensive linear algebra, but for the remainder of the tutorial, we’ll simply explain the intuition of SVMs. In general, SYM can be classified into two types they are
Linear SVM is used for a simple dataset where the data points can be categorized into two classes using a single linear line. Such data points are termed linear data and such algorithms are called Linear SVM classifiers.
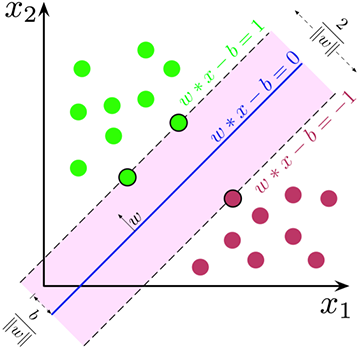
With a linear SVM, the goal is to draw a straight line that best separates the two classes, which is accomplished by
While we’ve shown prominent examples where there is a perfect separation between classes, we should note that sometimes, we need to accept some errors. After all, if the SVM can perfectly separate data all the time, it would be overfitting and not generalize to other data sets. SVMs aim to maximize the separation of data points and allow some erroneous data points to be classified.
Suppose we have a dataset with data of green and pink points. So we need an algorithm that can classify the green and pink points according to the x and y coordinates, where the x and y are the features of the dataset.
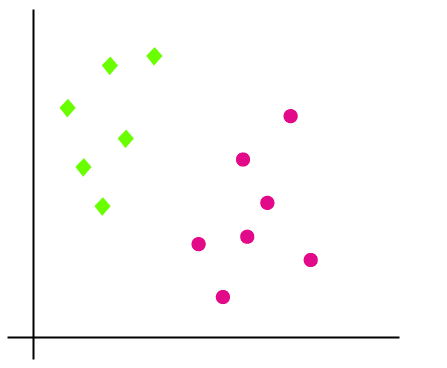
Now let us check it is a 2D plane and we can separate the data points using a linear line and can classify them into two classes but we can draw more than one linear line in this case just like this picture.
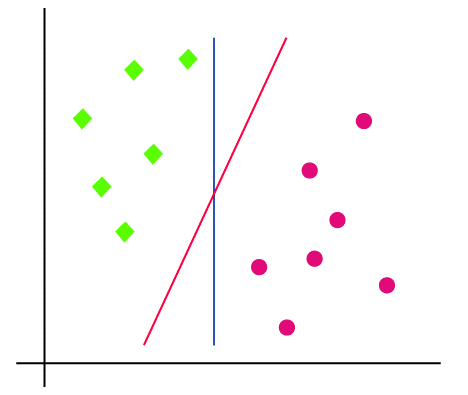
So the question arises which will be the perfect line to classify the data points and there comes the SVM into the picture. SVM helps to draw the best line that is called a hyperplane. After finding the line which is called as decision boundary, the SVM will find the closest point in both the categories with the hyperplane, and that is called support vectors. Now there will be a gap in between the hyperplane and support vector, which will be called as margin. The main objective of the SVM is to maximize the margin and it will be called an optimal hyperplane.
Nonlinear SVM is used for data that is not linear which means the dataset cannot be divided using a linear line. Such algorithms that we used to categorize the nonlinear data are called non-linear SVMs.
Suppose the raw data is not linearly separable as is. One way to approach this problem is to transform the data to be linearly separable by projecting the data into a higher-dimensional space. To visualize what this means, suppose we have the following data distribution between two classes.
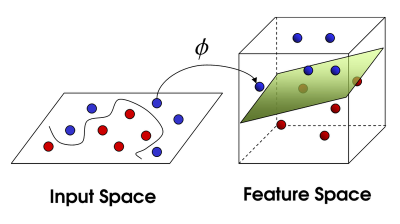
The data distribution on the left is tough to model using a linear model in a two-dimensional plane. However, if we extend the data to a higher dimension using the function? it becomes possible to draw a hyperplane that can separate the purple from the orange points.
This powerful method of adding dimensionality to a dataset is called a kernel function. Many kernels can be applied for different data structures, and it is a hyperparameter that needs to be considered to optimize an SVM model.
1. SVM offers great accuracy
2. SVM works fine with all dimensional space
3. SVM uses very little memory and resources
4. Cost-effective
1. High training time which is not good in large data
2. It fails or give error prediction if the data is with overlapping classes
1. Face observation and detection
2. Text and hypertext arrangement
3. Bioinformatics