


In this tutorial you will master all about Python Sets; how to write set, how sets work in python, how to perform standard operations like union, intersection, and difference on set. Besides these, we will learn about the methods to manipulate sets.
Mathematically a set can be defined as a collection of distinct objects in an unordered fashion. Similarly, in python, A set is an unordered collection of unique elements. To be clear the elements in a set are not stored in memory as in the order they appear in the set. All elements in a set must be immutable. But the set itself is mutable so we can modify the set through the addition or removal of elements.
Another variant, called a frozen set, as its name refers is static and is immutable.
A set can be defined in two ways either by enclosing comma-separated elements in curly braces or by using the set() function.
Immutability is more accountable in sets than other data types because a set is mutable while elements in sets are immutable. This means we cannot change the elements once it is created. More precisely, Immutable data types like integer, float, string, tuple, etc can be an element in the set but never should be a list, set, or dictionary as they are mutable (changeable). A set can contain any number of elements.
Empty Set: Usually an empty set is defined using the set() function with zero arguments to avoid the ambiguity caused while using empty curly braces {}. Python accounts empty curly braces {} as a dictionary, another datatype in python which you will learn in the next tutorial.
emp_set=set()
print(type(emp_set))
emp_set={}
print(type(emp_set))
Output:
<class 'set'> <class 'dict'>
Homogenous Set: A Set with elements of the same immutable datatype.
int_set = {1,2,3,4}
print("Homogenous set with integer elements:",int_set)
str_set = {'red','blue','green'}
print("Homogenous set with string elements:",str_set)
Output:
Homogenous set with integer elements: {1, 2, 3, 4}
Homogenous set with string elements: {'green', 'blue', 'red'}
Mixed Set: Set with elements of a different immutable datatype
mix_set={3.14,'prime',(1,2,3,5,7)}
print("Mixed set is ",mix_set)
Output:
Mixed set is {3.14, 'prime', (1, 2, 3, 5, 7)}
In python, a set is typically used to validate the membership of elements and to eliminate duplicates from a sequence. We have learned that the python set does not reckon duplicate elements and mutable elements. If any duplicate element is present in a set then it will automatically eliminate the duplicates from the sequence and similarly, if any mutable element is included in a set, Python will raise a TypeError as shown in the below
S={1,2,3,1,2,3} # duplicate elements are automatically eliminated
print (S)
Output:
{1, 2, 3}
Example: mutable elements in the set
S={ 'odd',[1,3,5]}
print(S)
Output:
TypeError: unhashable type: 'list'
From the above example, we could understand that list is unhashable. So what do you meant by hashable? Hashable means able to hash which in turn tells that object or datatype is fixed and it cannot be changed once it is created. An element is hashable if the element is immutable. For example string, a tuple is immutable and hence is hashable. In contrast, Python List which is a mutable element is unhashable.
Note: Immutable objects are hashable while mutable is not.
We are now familiar that a set is an unordered collection of elements that are unique. The way set members are stored is not the same as they appear on the set. To understand let’s examine the below example.
A=set('Green')
print(A)
Output:
{'e', 'G', 'n', 'r'}
Also, we can find that it eliminated the duplicate value ‘e’ from the set(‘Green’) and returns the set with four unique elements,
{'e', 'G', 'n', 'r'}.From this, we can infer that it is not possible to access elements from a list using indexing and slicing as done for other data types like string and tuple.
The mutable behavior of a set makes it possible to modify the set by adding individual or group elements. Two common methods used to add elements to a list are :
str_set = {'red','blue','green'}
str_set.add("Black")
print("New set after addition :",str_set)
Output:
New set after addition : {'blue', 'green', 'red', 'Black'}
str_set = {'royal blue'}
str_set.update((65,105,225))
print("New set after addition :",str_set)
Output:
New set after addition : {65, 'royal blue', 225, 105}
To remove an element from a set there are two methods available in the python set. They are discard() and remove(). The only behavior that distinguishes discard() from remove() is that if an element is not available in the set, discard() leaves the set as it is, however, the remove() raises a KeyError. This can be illustrated in the below example.
A= {1,2,3,4,6,8}
A.discard(3)
print(A)
A.remove(4)
print(A)
A.discard(5)
print(A)
A.remove()
print(A)
Output:
{1, 2, 4, 6, 8}
{1, 2, 6, 8}
{1, 2, 6, 8}
KeyError: 3
To remove entire elements from a set, we can use the clear() method. We can also use pop() the method to remove the last element in a set. As the set is unordered we can’t predict the result after pop(). To delete the entire set we can use the del keyword.
A= {1,2,3,4,6,8}
A.pop()
print("Set after using pop method is",A)
A.clear()
print(A)
del A
Output:
Set after using pop method is {2, 3, 4, 6, 8}
set()
Note: The return value of the pop() method is unpredictable as the set is unordered.
Set can be used for mathematical computation apart from the other uses like duplicate elimination and membership validation. The four common set operations are union, intersection, difference, and symmetric difference. We can perform these operations in python by using methods also.
Adding two sets in python simply means combining two different sets into a single set. Two sets can be joined using the set operation called Union. As its name, union unites two varying sets to a new set. The union operand used in python is “|” .If A and B are two sets then the union of A & B is represent as A|B.
Let our sets be

Union of A and B will be a new set with all unique elements in A and B. Duplicate elements are excluded from the set. Below shows the Venn diagram of A|B.
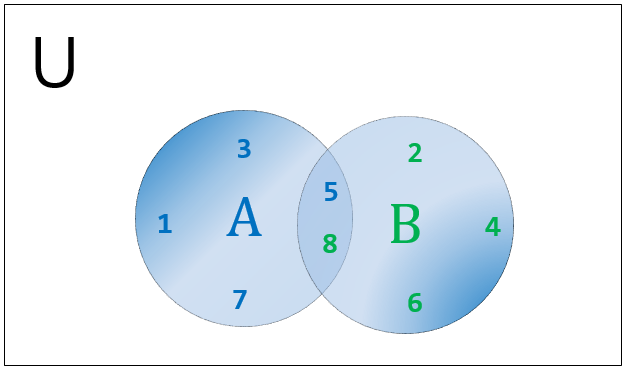
In python, the union of sets can be done in various ways. They are listed below
A = {1,3,5,7,8}
B = {2,4,5,6,8}
print("A|B = ",A|B)
print("A.union(B) = ",A.union(B))
print("B.union(A) = ",B.union(A))
Output:
A|B = {1, 2, 3, 4, 5, 6, 7, 8}
A.union(B) = {1, 2, 3, 4, 5, 6, 7, 8}
B.union(A) = {1, 2, 3, 4, 5, 6, 7, 8}
In the python intersection of two sets, A and B is the set consisting of common elements from both sets. The intersection of two sets can be denoted as A&B where & is the intersection operand.

Intersection of A and B returns the new set with common elements in A and B. In other words, we can say that duplicate values are taken as common elements. Below illustrated Venn diagram of A&B.
Python accomplish the intersection of sets either by using intersection operand or by using the intersection() method.
A = {1,3,5,7,8}
B = {2,4,5,6,8}
print("A&B =",A&B)
print("A.intersection(B) = ",A.intersection(B))
print("B.intersection(A) = ",B.intersection(A))
Output:
A&B = {8, 5}
A.intersection(B) = {8, 5}
B.intersection(A) = {8, 5}
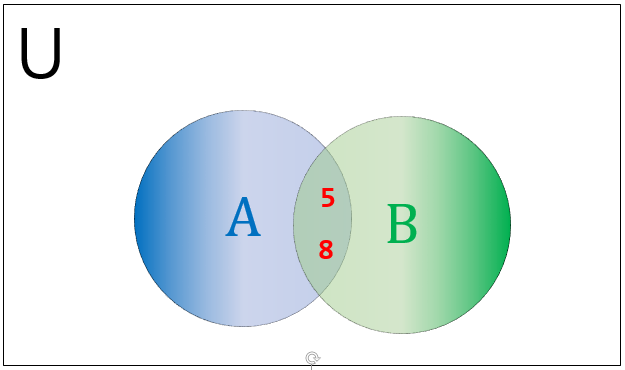
The difference in sets is quite a tricky concept than the usual mathematical difference. However, in both cases, we use the same operand(-) to denote the difference. To understand the concept undoubtedly consider A and B as two sets with distinct elements. The difference of set A and B can be denoted in two ways but they may not be equal.
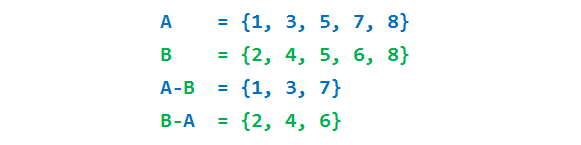
A Venn diagram to represent the difference of sets is illustrated below.
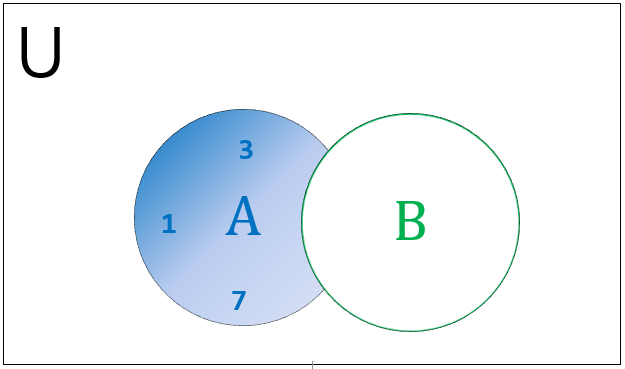
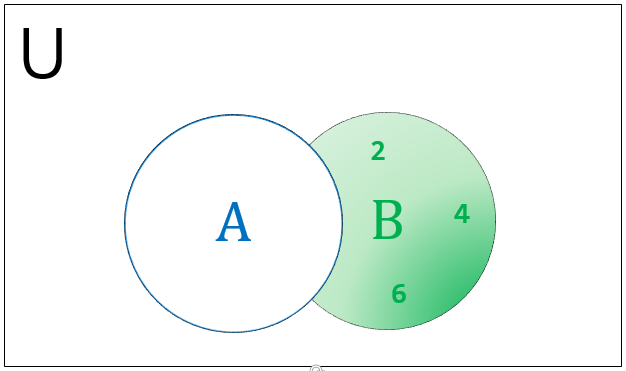
The set difference can be executed in python either using operand or difference() the method as shown in the below example.
A = {1,3,5,7,8}
B = {2,4,5,6,8}
print("A-B = ",A-B)
print("B-A = ",B-A)
print("A.difference(B) = ",A.difference(B))
print("B.difference(A) = ",B.difference(A))
Output:
A-B = {1, 3, 7}
B-A = {2, 4, 6}
A.difference(B) = {1, 3, 7}
B.difference(A) = {2, 4, 6}
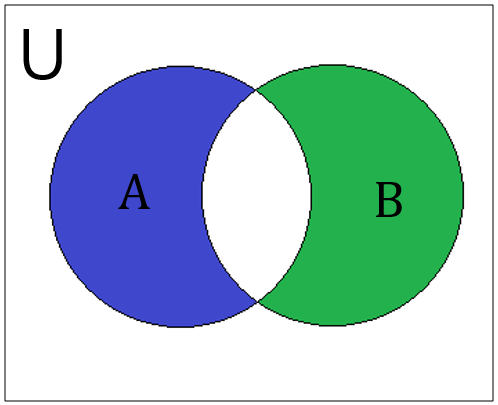
The symmetric difference in python is a set operation used to find the symmetric difference of two sets. Let A and B be two sets, their symmetric difference is the set consisting of elements in A and B but not in both. In another way, it is the union of A-B and B-A ie,
A^B =(A-B) |(B-A)the symmetric difference is of sets A and B can be represented as A^B where ^ is the operand. The method used is symmetric_difference().
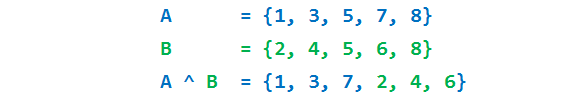
The symmetric difference can be best illustrated using a Venn diagram
The following example shows the working of symmetric difference.
A = {1,3,5,7,8}
B = {2,4,5,6,8}
print("A^B = ",A^B)
print("A.symmetric_difference(B) = ",A.symmetric_difference(B))
Output:
A^B = {1, 2, 3, 4, 6, 7}
A.symmetric_difference(B) = {1, 2, 3, 4, 6, 7}
Another important operation in the set is a validation of membership. This means we can easily check the presence of a subset of an element using membership operators. Two membership operators in python are :
A = {1,3,5,7,8}
print(3 in A)
print(8 not in A)
Output:
True False
Python set has some built-in functions to accomplish a variety of tasks. The following is a list of built-in functions with a set.
| Function | Description |
|---|---|
| len(Set) | Returns the number of elements in the set. |
| max(Set) | Returns the largest element in the set. |
| min(Set) | Returns the smallest element in the set. |
| sorted(set) | Returns a new set with elements sorted in ascending or descending order. |
| sum() | Returns the sum total of elements in the set. |
| enumerate() | Returns an enumerated object which is a pair of index and value for all the elements in set. |
| any() | Returns True if any element in the set is true and returns false for an empty set. |
| all() | Returns True if either all elements in the set are true or is an empty set. |
Python set has got plenty of methods to perform some specific tasks. Some of them we have familiarised with in the previous section. you can refer to the below table to acquaint with methods used with the set.
| Methods | Description |
|---|---|
| add() | Adds an element to the set |
| clear() | Removes entire elements from the set |
| copy() | Returns a copy of the set |
| difference() | Returns a new set comprising the difference of two or more sets |
| difference_update() | Updates the first set by removing common elements in the sets |
| discard() | Removes an element if it is present in the set otherwise does nothing |
| intersection() | Returns a new set that contains common elements of two sets. |
| intersection_update() | Updates the first set with common elements of two or more sets |
| isdisjoint() | Returns True if two sets have no common elements. |
| issubset() | Returns True if a set is present in the parent set. |
| issuperset() | Returns True if this set holds another set. |
| pop() | Removes the last element in a set. |
| remove() | Removes a particular element. |
| symmetric_difference() | Returns a set which is a symmetric difference of two sets |
| symmetric_difference_update() | Updates the first set with a symmetric difference of itself and other |
| union() | Returns a new set which is a combination of two or more sets. |
| update() | Updates the set with the union of an existing set and others. |
Another variant of the set is a frozen set, as its name indicates is a set with all its elements frozen. Unlike a set, all elements in the frozen set are fixed and are immutable (unchangeable) throughout its lifetime. Frozen sets are hence hashable which means their elements cannot be changed after their creation. The hash value of the frozen set can be used as a key for dictionary or as a set element for another set.
A frozen set is created using a frozenset() function. The parameter can be a set or any mutable object. If the parameter is empty, then the frozenset function will return an empty frozenset. The following examples give you the idea of how to create a frozenset.
Fset=frozenset(['prime',1,2,3,5,7])
print(Fset)
Emp_Fset=frozenset()
print(Emp_Fset)
Output:
frozenset({1, 2, 3, 5, 7, 'prime'})
frozenset()
Frozenset perform almost all the methods that work in a set like copy(), difference(), intersection(), symmetric_difference() ,union(), issubset(), issuperset() and isdisjoint(). Since frozenset is immutable, methods to add or remove elements is not applicable and if tries to alter frozenset, the result will be a TypeError.
Note: TypeError will be raised if we try to modify the frozenset.