


The binary search algorithm is also called the "half interval algorithm" or "logarithmic algorithm". It can be used to search from a large list of elements. It works faster on large lists than the smaller ones as in sequential search.
The algorithm finds the middle element and compares it with the search item, if not then divides the array into two. A left subarray, an array containing elements before the middle element, and a right subarray have elements next to the middle element. Now any of these subarrays will be chosen to continue the search according to the possibility of the search element being present. This process will continue until the result or the size of the sublist reduces to zero. It is thus using a divide and conquers method for searching an element in an array. The worst-case time complexity of Binary search is O(logn).
A binary search algorithm searches the element in a sorted array. If the given array is not sorted, the elements need to be sorted first before the search.
function could be written to implement binary search in R. The sorted array and search item can be passed as input variables to the function. and,while loop the middle element is computed first then checks the middle element with the search item if they are matched return index of middle element,return 0 as the last statement in the functionfunction with a sorted array, search value, and cat the results according to the return value from the functionNow, let's see the working of the Binary Search Algorithm.

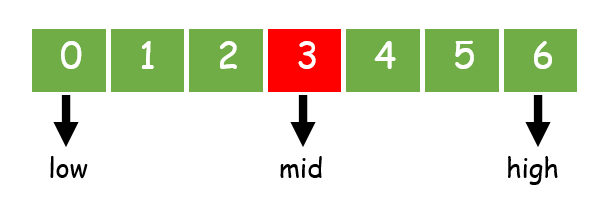
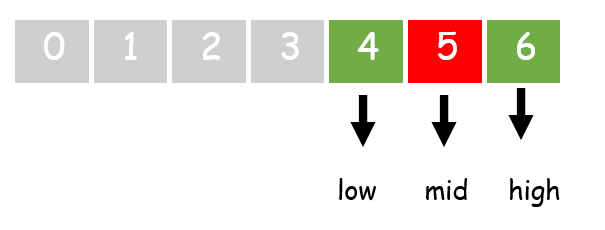
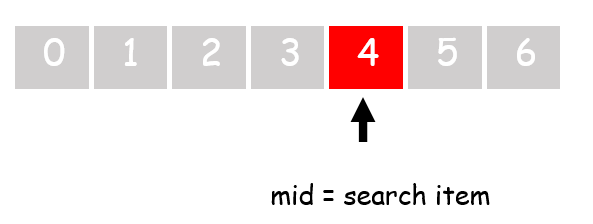
STEP 1: Write a function binarySearch() with variables array arr and search value item.
STEP 2: Initialise variables low 0 and high last index
STEP 3: Start a while loop to repeat until the condition low<=high,
STEP 4: Find the middle index of the array mid and check the middle element with the item, if matches return index of the middle element
STEP 5: Check if item<arr[mid] then last index becomes high=mid-1 else start index becomes low=mid+1
STEP 6: Now end the function by return 0 means no match was found
STEP 7: Initialise an array arr with values and item to be searched
STEP 8: Sort the array and call the binarySearch() with values arr, item and check the return value and cat the suitable result
binarySearch = function(arr,item) {
low <- 1; high <- length(arr)
while (low <= high){
mid <- as.integer(round((low + high) / 2))
if (abs(arr[mid] - item) ==0) {
return(mid)
} else if (arr[mid] < item) {
low <- mid + 1
} else {
high <- mid - 1
}
}
return(0)
}
arr <- c(4, 0, 3, 1, 5, 6, 2)
sorted_arr <- sort(arr)
item <- 4
cat("Array ", arr, "\nSorted array ",sorted_arr,"\nitem = ", item, "\n")
index <- binarySearch(sorted_arr, item)
if (index!=0){
cat("Element is present at index ", index, "\n")
}else{
cat("element not found")
}
Array 4 0 3 1 5 6 2 Sorted array 0 1 2 3 4 5 6 item = 4 Element is present at index 5