


Consider a situation where we are planning for our forward move but someone else is preparing against us and therefore our plans will be affected by this opponent’s activities. A method applied to such a situation is called adversarial search. The term search is referred to games in the domain of AI.
In our previous topics, we discussed searching strategies associated with a single agent. But there are situations where more than one agent works in a single environment. This kind of situation will occur mainly in game playing.
An environment with more than one agent is called a multi-agent environment (you can make a click to our 5th topic task environment for more details on the multi-agent environment). Here each agent will perform as an opponent for each other and will play against each other. Each agent must have to consider the actions of others and the effect of those actions on their performance.
So, Adversarial search can be defined as a game-playing technique where the environment of the agents is with a competitive feature. The agents are trying to explore the single search space for the solution. Adversarial searches can often be called games.
Examples: Chess, trading, War.
We change our state but then we don’t have any control over the next state. The opponent will change the next state in a way that they are unpredictable and opposing to us.
Mathematically, this searching method is based on the concept of ‘Game Theory’. According to this, a game is played between two or more players and one has to win the game and the others lose automatically to complete the game.
This searching method is one of the most important in the AI domain. It will provide solutions in multiple player environments with complex situations.
It will provide solutions for situations like
Adversarial search is made used in many areas and a few of the applications are listed below.
We already discussed some searching methodologies. For such normal searches, a sequence of actions is followed to reach the goal or to finish the game. But for an adversarial search, the result will depend on the players which will change the result or decide the result of the game. Since the player will try to win the game with the shortest path within the limited time the solution will be an optimal solution.
Following are the types of adversarial search
In AI, minimax is a decision-making strategy used in game theory to minimize the chances of losing and maximize the chances of winning. It is also called a saddle point. It is based on two players where if one wins the game the other will lose the game. It can be said as a kind of backtracking algorithm. The games that we play in our day-to-day life like Tic-Tac-Toe, Backgammon, Mancala, Chess, etc. simulate this strategy.
In the minimax strategy, the two players are named as minimizer and maximizer, where the maximizer tries to get the highest possible score and the minimizer tries to perform the opposite and the lowest possible score. It follows a DFS concept. The game here is played alternatively between the maximum and the minimizer. When the maximize made a move then the next move is for the minimizer. The move made by the maximize is fixed and cannot be changed. This concept is employed in the DFS strategy; the path cannot be changed in the middle.
Example
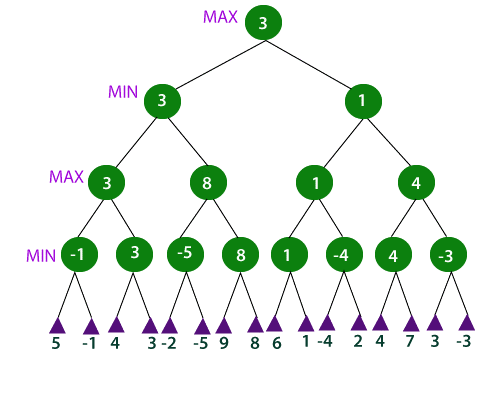
In the above example, the two players are MIN and MAX. MAXZ starts the game by choosing a path and exploring all the nodes of that path. MAX will then backtrack to the initial node and select the best path which offers the maximum utility value. After this, the turn goes to MIN. It also explores a path and will backtrack. Here MIN will select a path that could minimize the winning chance of MAX or the utility value.
| Advantages | Disadvantages |
|---|---|
|
|
Alpha-beta pruning can be said as an advanced form of minimax algorithm. The main fault of the minimax strategy is the heavy time consumption as it explores each node deeply to provide the best path among the others. Alpha-beta pruning will reduce this problem by a huge factor. This method allows us to search much faster and even deeper. It uses two extra parameters called alpha and beta in the minimax function. It also cut off the search by exploring a reduced number of nodes. The unwanted branches are pruned using the pruning technique. And hence called alpha-beta pruning. Here Alpha is the best possible value that the maximum can have at a particular level. And Beta is the best possible value that the minimizer can have at a particular level.
Example:
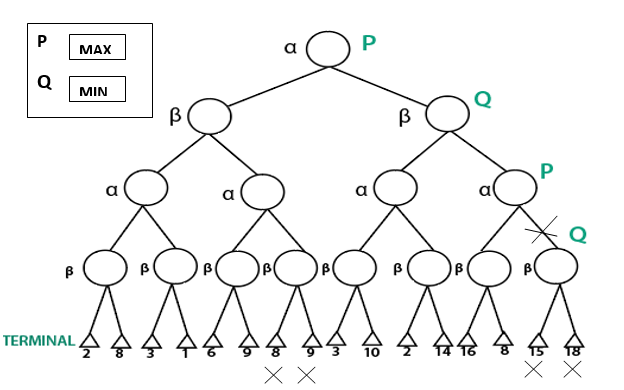
In the above figure, P and Q are two players. Let P be the one who tries to win the game by maximizing the winning chances and Q is the one who tries to minimize the winning chances of P. Here alpha represents the maximum value of the nodes and beta represents the minimum value of the nodes.
| Advantages | Disadvantages |
|---|---|
|
|