


Now you know what an uninformed algorithms is from our previous tutorial. Now another category of the searching strategy in AI is the informed search algorithms.
Informed search algorithms, as its name implies, contain information about the goal state which will make searches more efficient. It contains an array of knowledge about how close is the goal state to the present state, path cost, how to reach the goal, etc. Informed search algorithms are useful in large databases where uninformed search algorithms can’t make an accurate result.
Informed search algorithms are also called heuristic search since it uses the idea of heuristics.The heuristic function is a function used to measure the closeness of the current state to the goal state and heuristic properties are used to find out the best possible path to reach the goal state concerning the path cost.
Consider an example of searching a place you want to visit on Google maps. The current location and the destination place are given to the search algorithm for calculating the accurate distance, time taken, and real-time traffic updates on that particular route. This is executed using informed search algorithms.
Informed search algorithms can be classified into 4 major types.
It is a simple search performed based on a heuristic value denoted by h(n). It maintains two lists OPEN for new and unexpanded nodes and CLOSE for expanded nodes. The node with the smallest heuristic value is expanded for every iteration. And then all its child nodes are expanded and added to the closed list. A heuristic function is then applied to the closed list and the node with the shortest path is saved and the others are dispersed. The algorithm starts with the initial state node on the open list. Node with the minimum h(n) value on the open list is expanded at each cycle and generates its child nodes and is kept in the closed list. The heuristic function is then applied to the child nodes and is placed on the open list based on their heuristic values.
The procedure continues until the goal state is selected for expansion.
In pure heuristic search for a given heuristic function, The simplest method used is
f(n) = h(n)
where f(n) is the cost function and h(n) is the heuristic function. For a PHS algorithm, it doesn’t guarantee to terminate with an infinite graph even if there exists a goal node.
Example
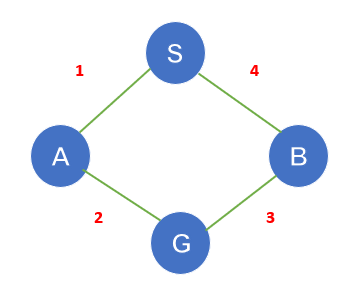
Here a solution of length 4 is returned even there exists one with length 3. PHS only considers h(n), the heuristic function or the estimated cost to the goal while expanding a node, or the cost to reach the goal node from the node n. It doesn’t consider the cost to reach node n from start state g(n)
| Advantages | Disadvantages |
|---|---|
|
|
As like the name best at first, is selected. It always selects the path which seems to be the best at that moment. It is a combination of both breadth-first search and depth-first search algorithms and takes the advantage of both algorithms. It also uses the heuristic function and performs the searching procedure. It helps to choose the most optimistic node at each step. The closest node to the goal node is expanded and the closest cost is approximated by the heuristic function.
Let us discuss with the help of traveling salesman problem.
A salesman is provided with a list of places to visit in a city. He has to find the optimum route to travel in such a way that the traveling time is reduced as much as possible. Here he can choose between 2 or more places from his current place to go to. He has to choose the one with the least distance.
Example,
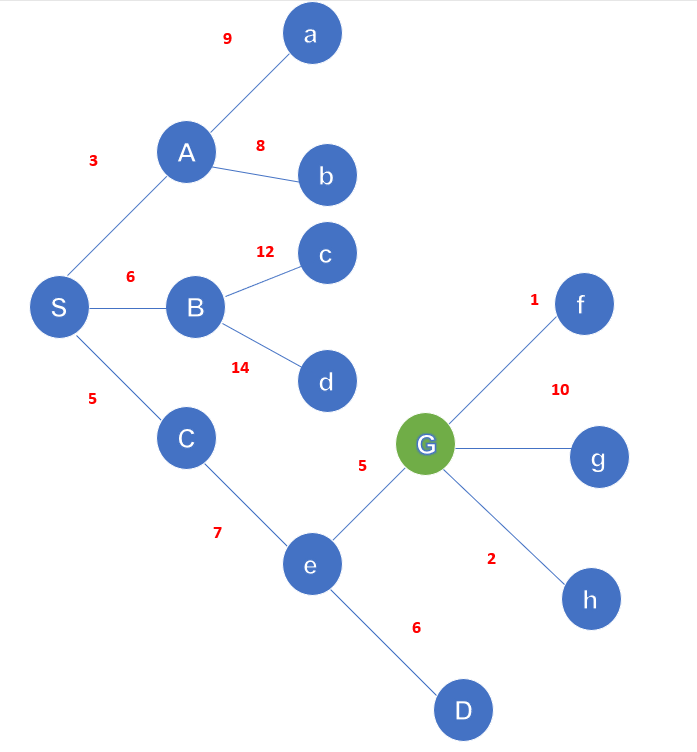
The node costs are stored in a priority queue pq.
The procedure can be like
Our source or starting node is S and the goal node is G. pq initially is with S. we remove S from pa and add the child node {A, C, B} (C is put before B because C is with less cost).
Now A is removed and a, b is added to pq {C, B, a, b}. Remove C and add e to pq {B, e, a, b} B is removed and c, d added to pq { e, a, b, c, d} . now e is removed since our goal has been reached
| Advantages | Disadvantages |
|---|---|
|
|
It combines the strength of both a greedy search and a uniform cost search (discussed in our previous topic). The heuristic of A* search is calculated as the summation of heuristic cost in greedy search and uniform cost search.
f(x) = h(x) + g(x)
The node with shortest f(x) is selected.
Example
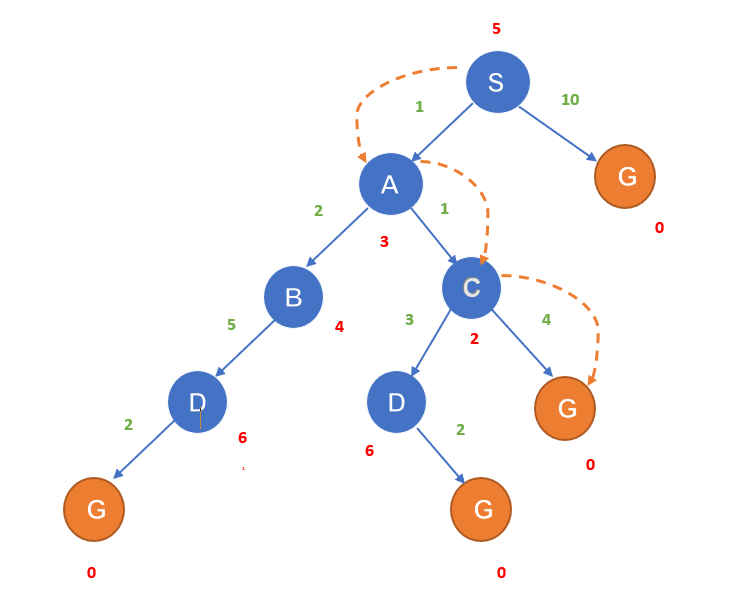
Here S is the initial node and G is the goal node. The numbers written on the edges(green) are the distance between the nodes and the numbers written on the nodes (red)are the heuristic values. The procedure starts from the node S. g(x) of S = 0, h(x) of S = 5. Therefore f(x) of S = 0 + 5 = 5.
Now from S, we can go to either A or G. f(x) for each node is computed.
S to A = 1 + 3 = 4
S to G = 0+ 10 = 10.
Since the cost for S to A is less we continue with this path.
A to B = 2 + 4 = 6
A to C = 1 + 2 = 3
Here the cost for A to C is less, continue with this path.
C to D = 3 + 6 = 9
C to G = 4 + 0 = 4
The Goal is reached
We conclude that S ---A---C---G is the most cost-effective path to get from S to G.
| Advantages | Disadvantages |
|---|---|
|
|
Considering the case of tree search, we do not keep this list and the same node is visited multiple times. Thus A* tree causes wastage of time by this multiple explorations. This limitation or the drawback can be removed or handled by using A*Graph search or simply Graph Search by adding the rule that does not expand a node more than once.
In graph searching we keep a list of explored sets to keep track of the expanded nodes, so that they are not visited again. A graph search can be said to be optimal only if the forward cost between two nodes say A and B given by h(A)-h(B) is less than or equal to the backward cost between those nodes given by g(A)-g(B). And this property of the graph searching technique is called consistency.
Example
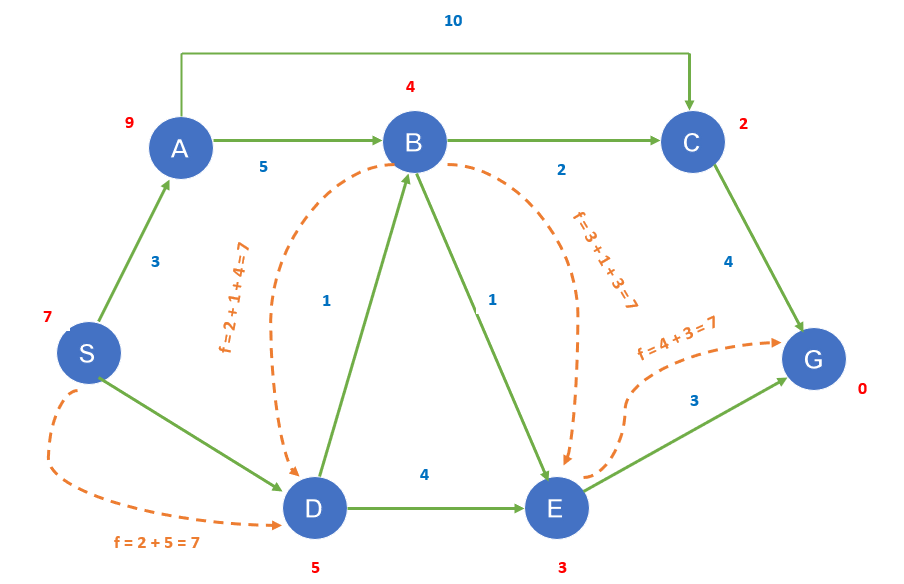
The solution is much like the tree method; the only difference is that a track of explored nodes is maintained so that they are never re-explored.
The initial node is S from there the path will be
From S to D
F= 2(S-D)+5(D)=7
F=2+5=7
D to B----- f= 2(S-D)+1(D-B)+4(B)=7
F=2+1+4=7
B to E-------- f= 3(S-D+D-B) + 1(B – E) + 3 (E) = 7
F= 3+1+3=7
E to G -------- f= 4 (S-D = D-B + B-E) + 3(E-G) + 0(G) = 7
F=4+3=7.
S----D---B---C---E---G
| Advantages | Disadvantages |
|---|---|
|
|